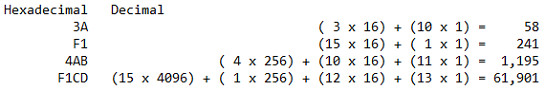Part 6: Hexadecimal Number System
For a complete table of contents of all the lessons please click below as it will give you a brief of each lesson in addition to the topics it will cover. https://github.com/mytechnotalent/Reverse-Engineering-Tutorial
Now that we are binary masters, it's time to tackle the numbering system of numbering systems!
We learned in binary that each number represents a bit. If we combine 8 bits, we get a byte. A byte can be further subdivided into its top 4 bits and its low 4 bits. A combination of 4 bits is a nibble. Since 4 bits gives you the possible range from 0 - 15 a base 16 number system is easier to work with. Keep in mind when we say base 16 we start with 0 and therefore 0 - 15 is 16 different numbers.
This exciting number system is called hexadecimal. The reason why we use this number system is that in x86 Assembly it is much easier to express binary number representations in hexadecimal than it is in any other numbering system.
Hexadecimal is similar to every other number system except in hexadecimal, each column has a value of 16 times the value of the column to its right. The fun part about hexadecimal is that not only do we have 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 we have A, B, C, D, E and F and therefore 16 different symbols.
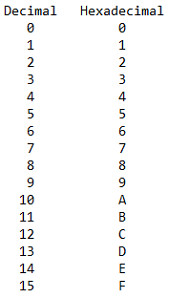
Lets look at a simple table to see how hexadecimal compares to decimal.
Ok I see the smoke coming out of your ears but its ok! In decimal, everything is dealt with in the power of 10. Let's take the number 42 and examine it in decimal:
2 x 10 ^ 0 = 2
4 x 10 ^ 1 = 40
Remember 10 to the 0 power is 1 and 10 to the 1st power is 10, therefore, 2 + 40 = 42.
Grab your coffee, here comes the fun stuff!
If we understand that decimal is a base 10 number system, we can create a simple formula where b represents the base. In this case, b = 10.
(2 * b ^ 0) + (4 * b ^ 1)
(2 * 10 ^ 0) + (4 * 10 ^ 1) = 42
In binary, 42 decimal is 0010 1010 binary as follows:
0 x 2 ^ 0 = 0
1 x 2 ^ 1 = 2
0 x 2 ^ 2 = 0
1 x 2 ^ 3 = 8
0 x 2 ^ 4 = 0
1 x 2 ^ 5 = 32
0 x 2 ^ 6 = 0
0 x 2 ^ 7 = 0
0 + 2 + 0 + 8 + 0 + 32 + 0 + 0 = 42 decimal
In hexadecimal, everything is dealt with in the power of 16. Therefore 42 in decimal is 2A in hexadecimal:
10 * 16 ^ 0 = 10
2 * 16 ^ 1 = 32
10 + 32 = 42 decimal => 2A hexadecimal
This is the same as saying:
10 * 1 = 10
2 * 16 = 32
10 + 32 = 42 decimal => 2A hexadecimal
Keep in mind 10 decimal is equal to A hexadecimal and 2 decimal is equal to 2 hexadecimal. In our formula above when we deal with A, B, C, D, E or F we need to convert them to their decimal equivalent.
Lets take another example of F5 hexadecimal. This would be as follows:
5 x 16 ^ 0 = 5
15 x 16 ^ 1 = 240
5 + 240 = 245 decimal => F5 hexadecimal
Lets look at a binary to hexadecimal table:

It is important to understand that every hexadecimal number is 4 bits long or called a nibble. This will become critical when we are reverse engineering our C programs into Assembly.
Lets look at this another way. Lets work with some more hexadecimal numbers and convert them to decimal:
To re-emphasize F1CD as a simple conversion:
D --- 13 x 1 = 13
C --- 12 x 16 = 192
1 --- 1 x 256 = 256
F --- 15 x 4096 = 61,440
13 + 192 + 256 + 61,440 = 61,901
Addition in hexadecimal works as follows. From this point forward all numbers in hexadecimal will have a 'h' next to the number:

Another example is as such:
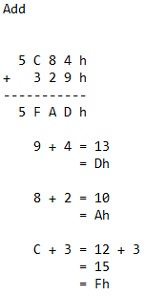
A final add example is as such:
We will now focus on subtraction:
You are probably asking yourself why is this guy spending so much time going over so many different ways of learning this! The answer is that each of us learn a little different from the next. I wanted to show several representations of hexadecimal compared to decimal and binary to help put together the whole picture.
It is fundamental that you understand what is going on here in order to proceed any further. If you have any questions, please comment below and I will be more than happy to help!
In our next lesson we discuss switches, transistors and memory.