Part 4 - Number Systems
For a complete table of contents of all the lessons please click below as it will give you a brief of each lesson in addition to the topics it will cover. https://github.com/mytechnotalent/Reverse-Engineering-Tutorial
It really all breaks down to 1 and 0. No matter how sophisticated the future frameworks evolve they all including interpreted languages ultimately use a JVM or the like and go down to Assembly then Machine Code then binary.
Why would we need to even talk about number systems? Why is it relevant to our series here? The answer is simple. In addition to everything going down to 1 and 0, the instructions and memory in addition to the processor registers all utilize another number system called hexadecimal.
Let’s discuss binary! At the core of the microprocessor are a series of binary numbers which are either +5V (on or 1) or 0V (off or 0). Each 0 or 1 represents a bit of information within the microprocessor. A combination of 8 bits results in a single byte.
Before we dive into binary, let's examine the familiar decimal. If we take the number 2017, we would understand this to be two thousand and seventeen.
Let’s take a look at the binary system and the basics of how it operates.
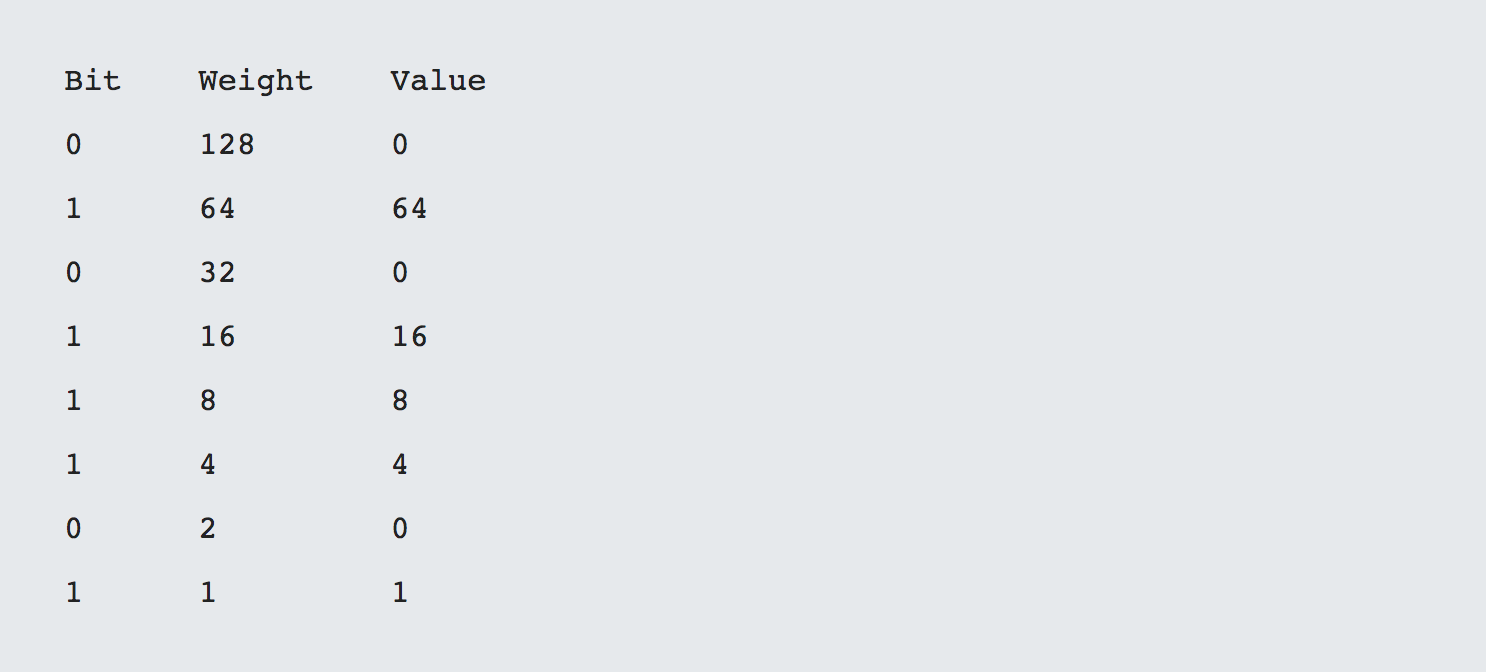
If we were to convert a binary number into decimal, we would very simply do the following. Let's take a binary number of 0101 1101 and as you can see it is 93 decimal.
Adding the values in the value column gives us 0 + 64 + 0 + 16 + 8 + 4 + 0 + 1 = 93 decimal.
If we were to convert a decimal number into binary, we would check to see if a subtraction is possible relative to the highest order bit and if so, a 1 would be placed into the binary column to which the remainder would be carried into the next row. Let’s consider the example of the decimal value of 120 which is 0111 1000 binary.
1)Can 128 fit inside of 120: No, therefore 0.
2)Can 64 fit inside of 120: Yes, therefore 1, then 120 – 64 = 56.
3)Can 32 fit inside of 56: Yes, therefore 1, then 56 – 32 = 24.
4)Can 16 fit inside of 24: Yes, therefore 1, then 24 – 16 = 8.
5)Can 8 fit inside of 8: Yes, therefore 1, then 8 – 8 = 0.
6)Can 4 fit inside of 0: No, therefore 0.
7)Can 2 fit inside of 0: No, therefore 0.
8)Can 1 fit inside of 0: No, therefore 0.
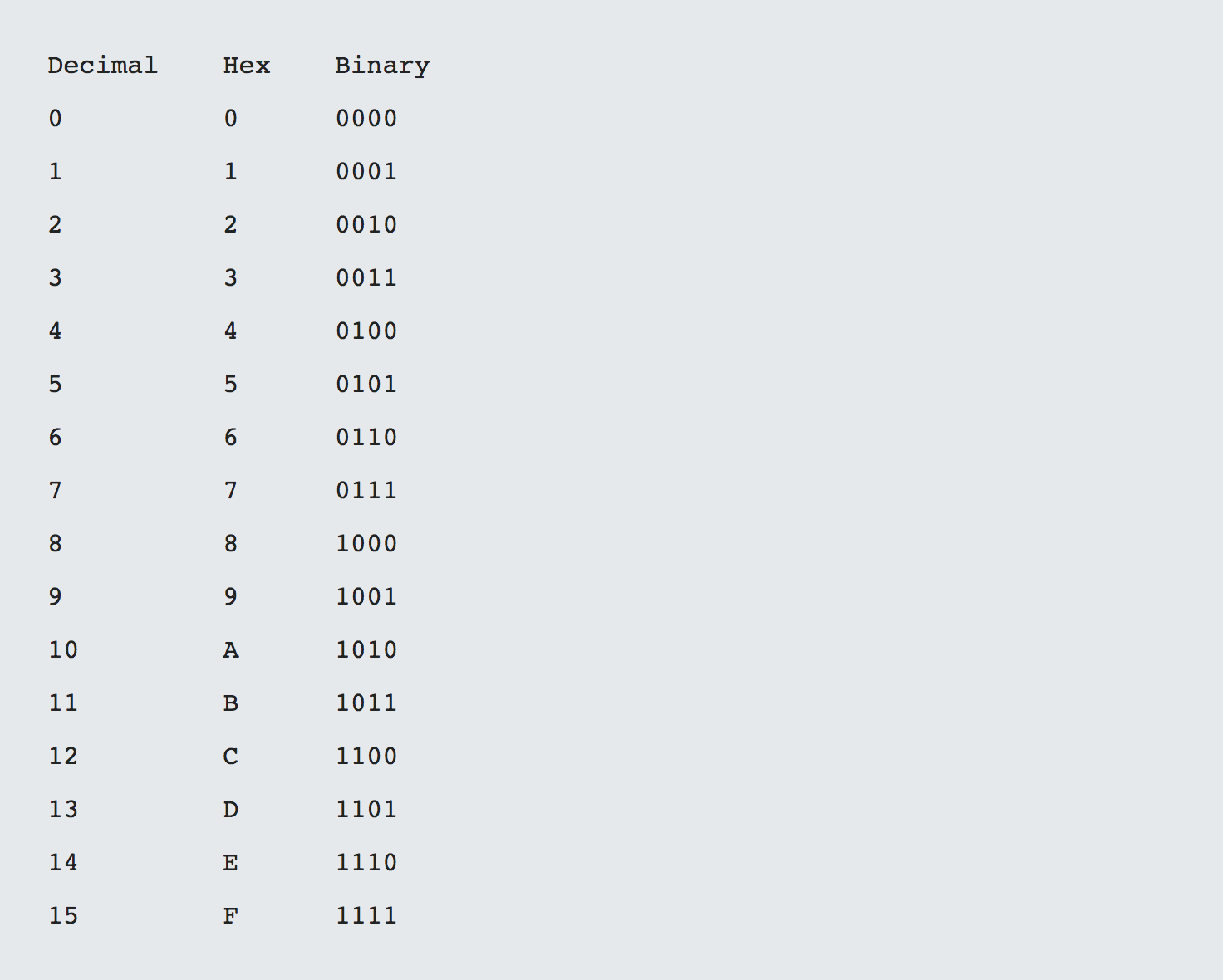
When we want to convert binary to hex we simply work with the following table.
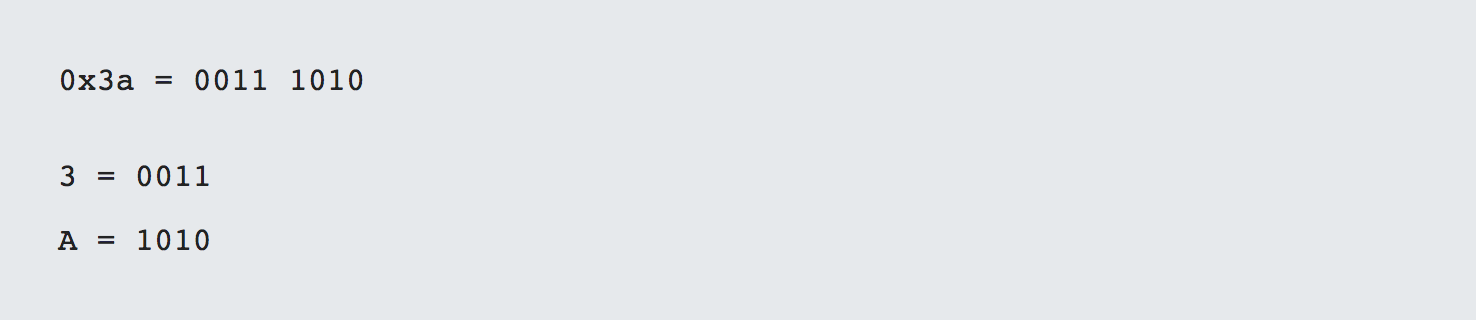
Let's convert a binary number such as 0101 1111 to hex. To do this we very simply look at the table and compare each nibble which is a combination of 4 bits. Keep in mind, 8 bits is equal to a byte and 2 nibbles are equal to a byte.
Therefore 0101 1111 binary = 0x5f hex. The 0x notation denotes hex.
To go from hex to binary it’s very simple as you have to simply do the opposite such as:
It is important to understand that each hex digit is a nibble in length therefore two hex digits are a byte in length.
To convert from hex to decimal we do the following:
Therefore we can see that 80 + 15 = 95 which is 0x5f hex.
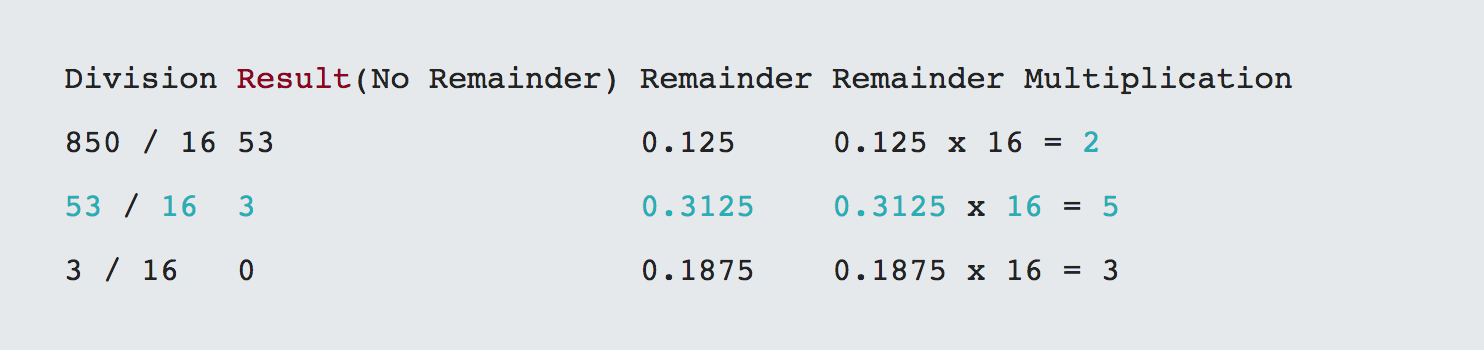
Finally to convert from decimal to hex. Let's take the number 850 decimal which is 352 hex.
“Why the hell would I waste my time learning all this crap when the computer does all this for me!”
As I mentioned above, it is vital you have a good understanding of these two additional number systems if you are truly to grasp and master reverse engineering at its core. There are some amazing tools that help the RE process however the better understanding that you have of these will help you as you grow.
I am not suggesting you memorize the above, nor am I suggesting that you do a thousand examples of each. All I ask is that you take the time to really understand that literally everything and I mean everything goes down to binary bits in the processor.
Whether you are creating, debugging or hacking an Assembly, Python, Java, C, C++, R, JavaScript, or any other new language application that hits the street, ultimately everything MUST go down to binary 0 and 1 to which represent a +5V or 0V.
We as humans operate on the base 10 decimal system. Let’s expand our mind to base 2 binary and base 16 hexadecimal!
Next week we will dive into binary addition! Stay tuned!